Einleitung

Unser Problem: Wir möchten ein Objekt (z.B. einen Ball) in jede Richtung über den Bildschirm bewegen lassen. Bis jetzt haben wir eine Richtungsvariable, die 8 Richtungen speichert. Mit einer Select Case Abfrage kann man nun entsprechend die Koordinaten verändern.
Beispiel:

Global richtung=1	;Richtungsvariable
			;1 ... oben
			;2 ... oben rechts
			;3 ... rechts
			;4 ... unten rechts
			;5 ... unten 
			;6 ... unten links
			;7 ... links
			;8 ... oben links
...
While Not KeyHit(1)
	...
	Select richtung
		Case 1:	y = y - 1
		Case 2: y = y - 1 : x = x + 1
		Case 3: x = x + 1
		Case 4: y = y + 1 : x = x + 1
		Case 5: y = y + 1
		Case 6: y = y + 1 : x = x - 1
		Case 7: x = x - 1
		Case 8: y = y - 1 : x = x - 1
	End Select
	...
Wend
End

Ziemlich schnell werden 2 Probleme auffällig:
a) Wir haben nur 8 Richtungen, was für den Anfang nicht schlecht ist. Aber 360 Richtungen sind problemlos möglich.
b) Bei diagonalen Bewegungen (z.B. oben links) ist unser Objekt viel schneller als beispielsweise bei einer horizontalen (links/rechts). Das ist auf den ersten Blick wunderlich, aber nach einer kleinen mathematischen Rechnung logisch: Bei der Richtung 3 (rechts) bewegt sich das Objekt 1 Pixel nach rechts. Bei der Richtung 4 bewegt es sich allerdings 1 Pixel nach rechts und ein 1 Pixel nach unten. Mit dem Satz des Pythagoras macht das Wurzel aus 2 Pixel (~ 1.4). Dadurch erscheint es deutlich schneller.
Alle beide Probleme (a,b) lassen sich mit Winkelrechnung einfach lösen. Aber erst mal zur mathematischen Theorie.

Vorbetrachtung

Wie der Name Winkelfunktion schon vermuten lässt, sind sowohl Sin() (Sinus) und Cos() (Kosinus) von einem Winkel abhängig. Am besten zeigen lässt sich diese Abhängigkeit an einem Kreis. Dazu benutzen wir einen Einheitskreis, welcher simplerweise ein Kreis mit dem Radius 1 ist. (In der Geometrie mit der Einheit cm, bei uns natürlich in Pixel).
Zunächst ein Bild zum besseren Verständnis:

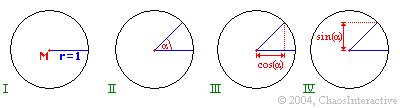
I.

Hier sehen wir den Einheitskreis mit dem Mittelpunkt. Die blaue Linie soll einerseits den Radius von einer Längeneinheit verdeutlichen, andererseits steht er auch für den Winkel 0°. Das heißt, die Linie die nach rechts zeigt, hat den Winkel 0°. Anhand dieser Festlegung kann man den Winkel anderer Linien relativ zu dieser blauen bestimmen.

II.

Jetzt ist eine andere Linie dazu gekommen. Der Winkel dieser Linie wird durch den Winkel zwischen ihr und der nach rechts zeigenden Linie angegeben. In diesem Fall entspricht der Winkel 45°. Würde diese Linie nach oben zeigen, wäre Alpha (also der Winkel) 90° groß. Wichtig: In der Mathematik ist der Richtungssinn entgegengesetzt dem Uhrzeigersinn. Deswegen hätte eine Linie, die nach unten zeigt den Winkel -90°. Logischerweise wäre der Winkel 360° der gleiche wie 0°. Auch die Linien mit dem Winkeln 270° und -90° würden in die gleiche Richtung zeigen.

III.

Jetzt wird es interessant. Wir sehen immer noch die 2 Linien. An dem Punkt, wo die obere Linie (mit dem Winkel 45°) zu Ende ist, wird vertikal ein Lot zur 0°-Linie geworfen. (Ist ziemlich blöd zu erklären, aber durch das Bild III hoffentlich einleuchtend.) Die Strecke zwischen dem Punkt, auf dem das Lot (die gepunktete rote Linie) die 0°-Linie schneidet und dem Mittelpunkt M entspricht dem Kosinus von Alpha. In diesem Fall also cos(45°).
Kleine Rechnerei: Wir wissen, dass die 0°-Linie die Länge 1 hat. Im Bild sehen wir, dass das Lot nach der Hälfte der 0°-Linie erst "aufschlägt". Der Kosinus müsste also einen Wert zwischen 0.5 und 1 haben. Stimmt auch: ~.71.

IV.

Das ganze in Hellgrün für den Sinus. Denkt man sich eine horizontale Linie (im Bild rot gepunktet) und misst den kürzesten Abstand zwischen ihr und dem Mittelpunkt, so entspricht dieser dem Sinus des Winkels Alpha. Bei uns also sin(45°). Übrigens hat der Sinus von Alpha die gleiche Länge wie unser Lot aus Bild III. Bei dem Winkel den wir haben, ist eine Besonderheit festzustellen, die man auch mit dem bloßen Auge feststellen kann. Der Sinus von 45° ist gleich dem Kosiuns von 45°. (sin(45)=cos(45))

Anderer Erklärungsversuch

Eigentlich ist es ganz einfach, nur umständlich zu erklären. Also falls bei euch der Groschen noch nicht gefallen ist, werden wir mal ein bisschen unmathematisch. Nehmen wir an unser Punkt M aus Bild I hat die Koordinaten (0;0). Also hat das rechte Ende unserer blauen Linie die Koordinaten (1;0), da sie ja die Länge 1 hat. Wie oben beschrieben ist das ja die 0°-Linie. Ihr Winkel beträgt also 0°. Der Kosinus von 0° ist 1. Der Sinus von 0° ist 0. Dies hat zur Folge, das wir jeden Punkt bestimmen können, an dem eine blaue Linie mit dem Winkel Alpha und der Länge 1 endet. In den Bildern II bis IV endet die obere blaue Linie (Alpha beträgt hier ja 45°) also bei der Koordinate (cos(45°);sin(45°). Hier erkennt man nun den Zusammenhang zwischen Cos und Sin. Cos benutz man für die Berechnung der X-Koordinate und Sin für die der Koordinate. (Anmerkung: Vertauscht man das, ändern sich die Richtungen. Dies sollte vermieden werden.)

Beim Programmieren

Vorweg erst mal ein großer (hoffentlich bereits bekannter) Unterschied zwischen einem mathematischen Koordinatensystem und den Koordinaten eines Bildschirms beim Programmieren: In der Mathematik nimmt der Y-Wert nach oben hin zu. Auf dem Bildschirm nimmt er nach unten hin zu. Zu erkennen, dass der Punkt oben links die Koordinaten (0;0) hat und der Punkt unten rechts z.B. die Koordinaten (800;600). Würde man bei der Rechnung mit dem Sinus also mathematisch korrekt bleiben wollen (und das wollen wir, da wir uns eventuell eine Zukunft als Programmier vorstellen können...), müsste man immer den -Sin(winkel) nehmen.
Weiterhin ist zu beachten: Man gibt in Blitz Gradzahlen natürlich ohne dem °-Zeichen ein. Also Cos(45) statt Cos(45°).
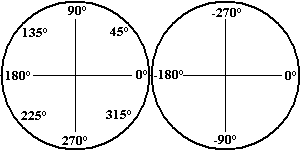
Zur Abwechslung mal wieder ein Bild, welcher Winkel welcher Richtung in BlitzBasic entspricht:

Jetzt sind genug Grundkenntnisse vorhanden, so dass ich euch eigentlich gleich an einem Quellcode die Benutzung des Ganzen zeigen kann. Was mein Programm macht: Man sieht einen Kreis mit einer Linie, die aus dem Mittelpunkt in eine bestimmte Richtung zeigt. Drückt man die Pfeil-Nach-Oben Taste, bewegt sich der Kreis die Richtung der Linie. Mit Links/Rechts kann man diese Richtung verändern.
Hier der Quellcode:

Graphics 800,600,32,2
SetBuffer BackBuffer()
Global w=0
Global x#=400, y#=300


While Not KeyHit(1)
	Cls

	Text 10,10,"Winkel: "+w

	Oval x#-5,y#-5,10,10,1
	Line x#,y#,x#+20*Cos(w),y#-20*Sin(w)


	If KeyDown(203) Then w=w+1
	If KeyDown(205) Then w=w-1
	If KeyDown(200) Then
		x# = x# + Cos(w)
		y# = y# - Sin(w)
	EndIf	


	Flip
Wend
End

Erläuterungen

Als Grundlage dient ein normales Grundgerüst (Graphics, SetBuffer, While...Wend-Hauptschleife). Als Variablen setzen wir die Ganzzahl w für den Winkel und die Gleitkommazahlen x# und y# für die Position des Kreises. Wichtig ist, dass diese keine Ganzzahlen sein dürfen, da sowohl Sin und Cos Kommazahlen zwischen -1 und 1 zurückliefern. Was passiert, wenn man dennoch Ganzzahlen nimmt, kann ja problemlos ausprobiert werden.
Das Zeichnen des Kreises ist ja noch nicht außergewöhnlich. Die Linie allerdings schon. Wir zeichnen die Linie von x#;y# (also dem Mittelpunkt des Kreise) zu x# + 20 * Cos(w) ; y# - 20 * Sin(w). Das bedeutet, dass wir eine Linie zeichnen, die exakt 20 Pixel lang ist und in die Richtung des Winkel zeigt. Hier bitte wie oben angesprochen darauf achten, dass der Kosinus zwar addiert, der Sinus jedoch subtrahiert wird.
Die nächste Anwendung der Winkelfunktionen findet statt, wenn wir Pfeil-Nach-Oben (Scancode 200) drücken. Mit x# = x# + Cos(w) und y# = y# - Sin(w) wird der Kreises exakt um einen Pixel in Richtung des Winkels verschoben. Will man nun allerdings den Kreis um 2 oder mehr Pixel verschieben, multipliziert man den Cos bzw. Sin einfach noch mit der gewünschten Länge (wie bei der Linie).

Das war's erst mal. Viel Spaß beim rumprobieren!

Winkelfunktion für Spieleprogrammierung